Как измерить длину коаксиального кабеля и его волновое сопротивление с помощью осциллографа.
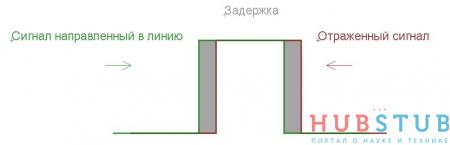
Для того чтобы передавать информацию через линию передачи данных необходимо, что бы сопротивление нагрузки было равно, волновому сопротивлению линии. Если это условие не выполнено и сопротивление нагрузки на конце линии велико, то энергия сигнала, дойдя до конца линии, не сможет выйти из неё и отразится обратно. Отражённый сигнал спустя некоторое время вернётся ко входу линии и сложится с сигналом, направленным в линию в итоге форма, передаваемого сигнала будет искажена, а информация потеряна.
Зная время, которое сигнал был в пути и его скорость можно вычислить расстояние, которое он прошёл. Скорость распространения сигнала по коаксиальному кабелю равна 2/3 скорости света, в среднем считается, что за 1 nS сигнал проходит 20 cm, на самом деле чуть меньше.
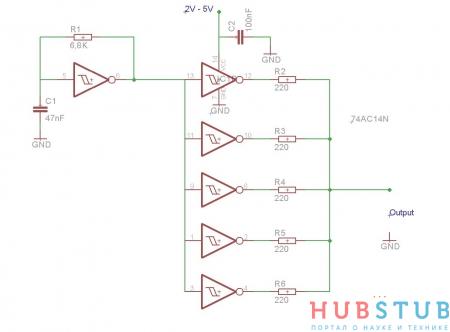
Для этого эксперимента нам потребуется собрать генератор меандра, с крутым фронтом.
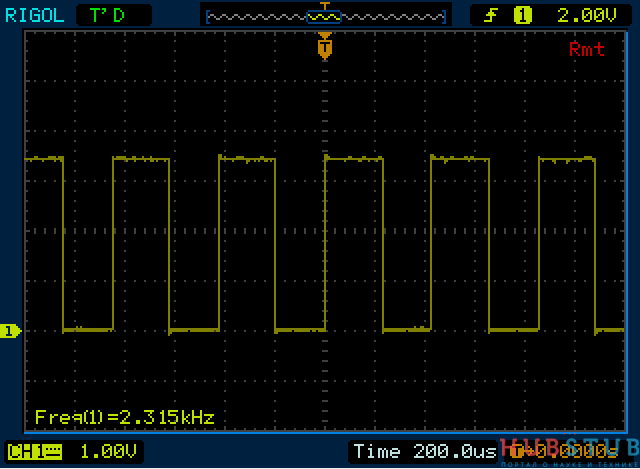
Время нарастания сигнала в такой схеме составляет несколько nS, у меня получилось 3,4 , а частота в зависимости от партии микросхемы колеблется от 2 до 6 KHz.
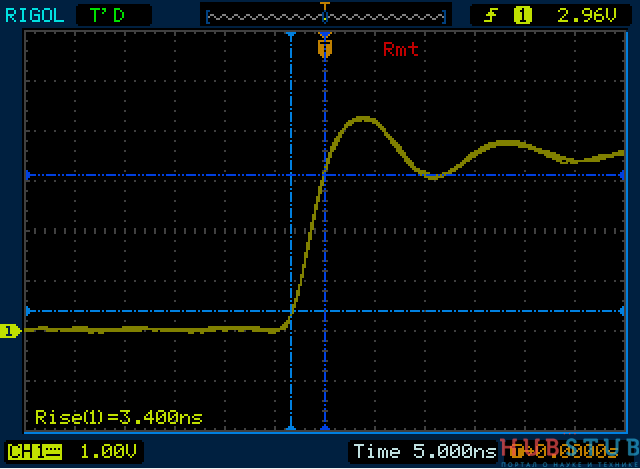
Схема изготавливается из двух кусков текстолита, на одном распаивается микросхема, в другом закрепляется BNC разъём.
С помощью Т-образного BNC коннектора подключим генератор и исследуемый кабель к осциллографу, длина кабеля 157 cm.
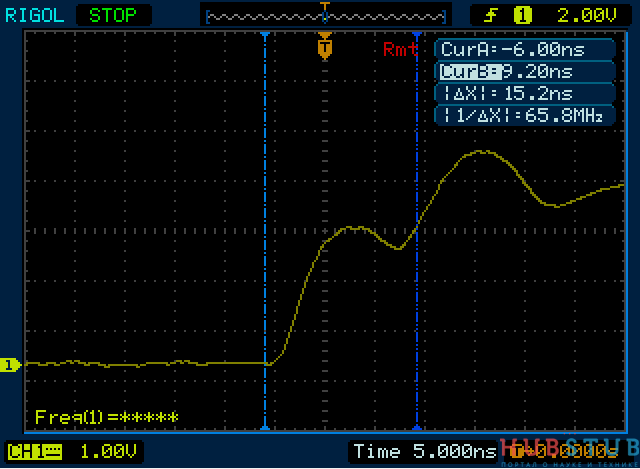
На осциллограмме видна некоторая задержка при нарастании фронта. Она возникает в месте где амплитуда сигнала, направленного в линию максимальна, а амплитуда отражённого сигнала равна нулю. Пока отражённый сигнал достиг начала линии, он прошёл путь равный 314 cm. Таким образом, время задержки должно быть равно 15,7 nS, измеренное время задержки равно 15,2 nS, разница обусловлена погрешностью метода.
Давайте к другому концу кабеля подключим подстроечный резистор и посмотрим как будет изменяться осциллограмма в зависимости от сопротивления.
При совпадении сопротивления резистора с волновым сопротивлением кабеля, вся энергия сигнала будет беспрепятственно переходить из линии в резистор и "ступенька", которая возникала за счёт отражённого сигнала, должна исчезнуть.
Сопротивление резистора 0 Ohm.
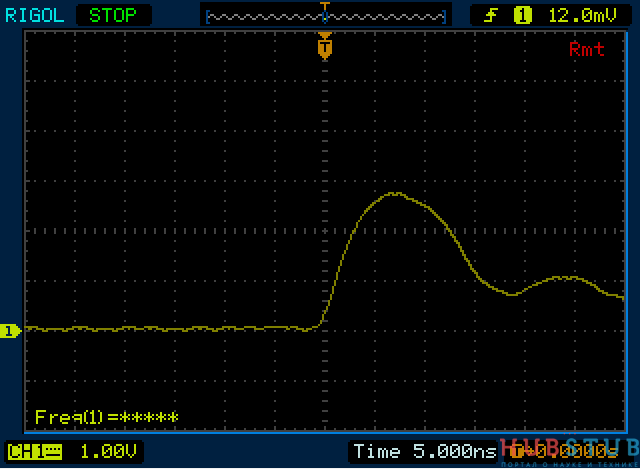
Сопротивление резистора 50 Ohm.
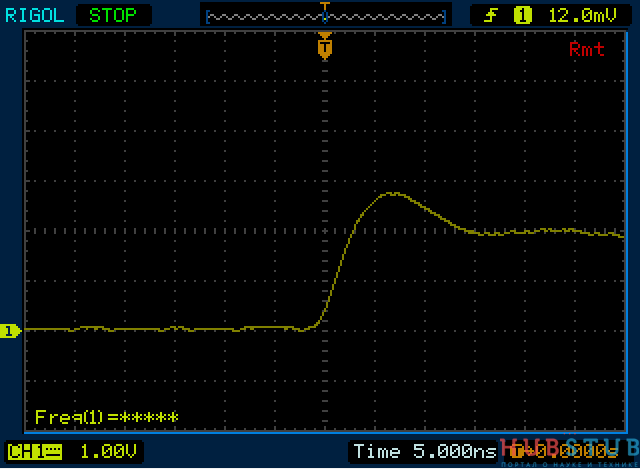
Сопротивление резистора 75 Ohm.
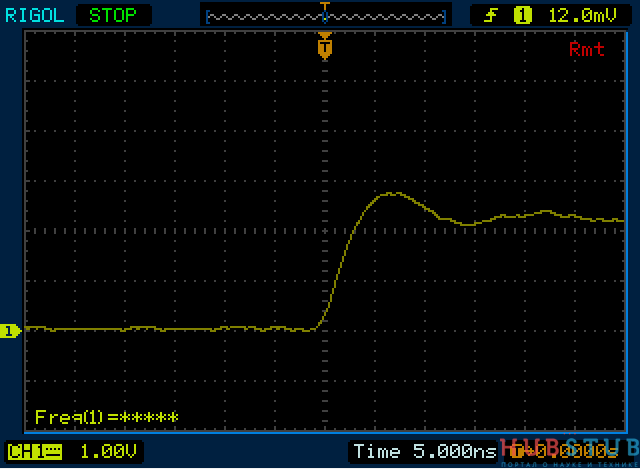
Сопротивление резистора 100 Ohm.
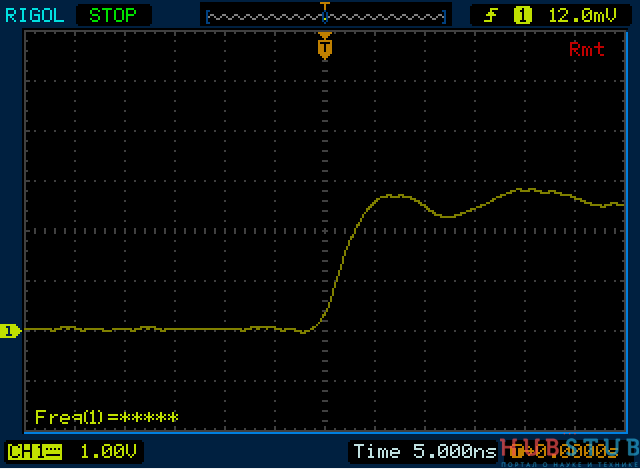
Из этих осциллограмм нельзя сделать однозначный вывод, какое волновое сопротивление этого кабеля.
Если увеличить длину кабеля, увеличится время задержки и изменение сопротивления на конце линии будет более наглядно. Длинного куска кабеля под рукой нет, но есть кабель, проложенный по плинтусу из одного помещения в другое. Подключил этот кабель к осциллографу с генератором.
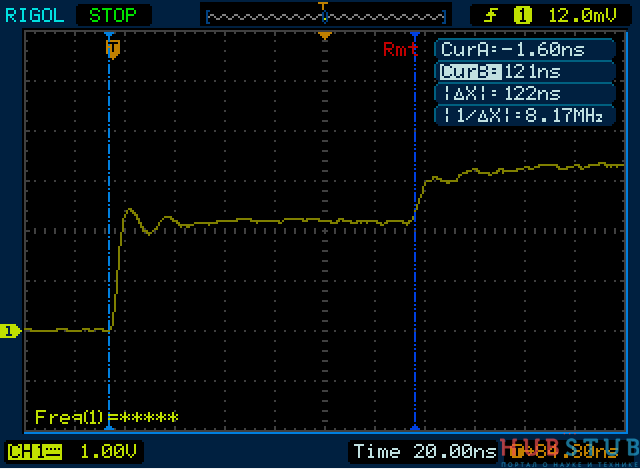
Длина "ступеньки" увеличилась, подпаиваем с другого конца сопротивление и начинаем крутить.
Сопротивление резистора 0 Ohm.
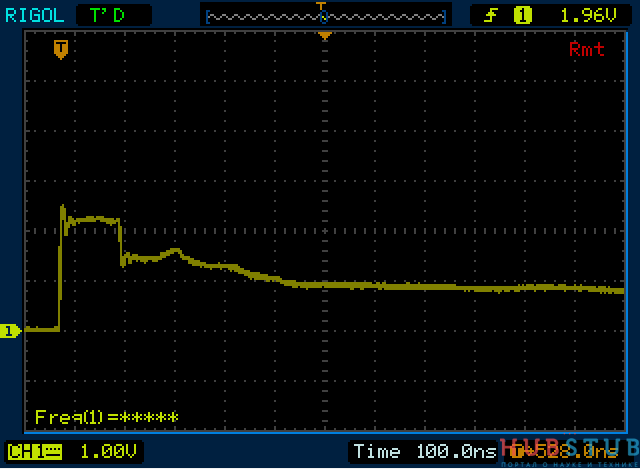
Сопротивление резистора 50 Ohm.
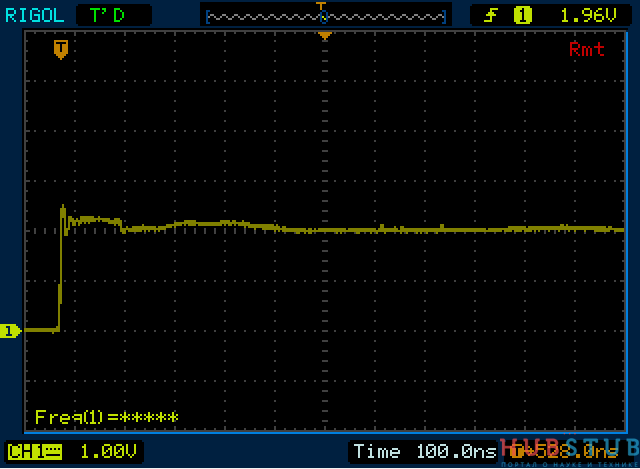
Сопротивление резистора 75 Ohm.
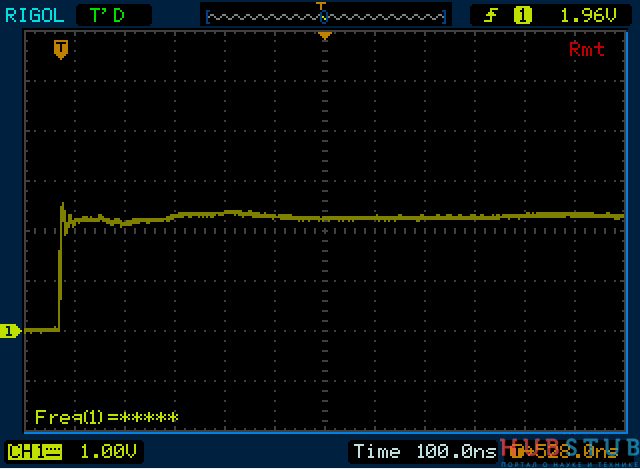
Сопротивление резистора 100 Ohm.
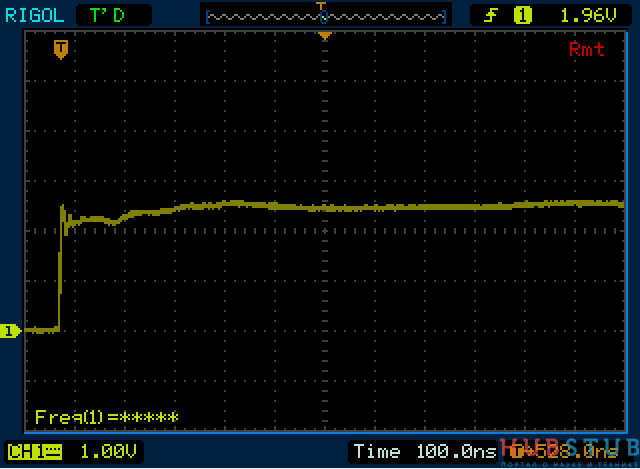
Из осциллограмм видно, что волновое сопротивление кабеля равно 75 Ohm, при других значениях сопротивления "ступенька" снова появлялась.
Опираясь на полученные знания можно вычислить скорость распространения сигнала, в любой другой линии передачи данных, измерив задержку в двухметровом куске. А зная скорость можно описанным способом вычислить длину более длинного кабеля.
Теперь мы знаем как измерить длину кабеля и его волновое сопротивление с помощью осциллографа.
Зная время, которое сигнал был в пути и его скорость можно вычислить расстояние, которое он прошёл. Скорость распространения сигнала по коаксиальному кабелю равна 2/3 скорости света, в среднем считается, что за 1 nS сигнал проходит 20 cm, на самом деле чуть меньше.
Для этого эксперимента нам потребуется собрать генератор меандра, с крутым фронтом.

Время нарастания сигнала в такой схеме составляет несколько nS, у меня получилось 3,4 , а частота в зависимости от партии микросхемы колеблется от 2 до 6 KHz.

Схема изготавливается из двух кусков текстолита, на одном распаивается микросхема, в другом закрепляется BNC разъём.
С помощью Т-образного BNC коннектора подключим генератор и исследуемый кабель к осциллографу, длина кабеля 157 cm.

На осциллограмме видна некоторая задержка при нарастании фронта. Она возникает в месте где амплитуда сигнала, направленного в линию максимальна, а амплитуда отражённого сигнала равна нулю. Пока отражённый сигнал достиг начала линии, он прошёл путь равный 314 cm. Таким образом, время задержки должно быть равно 15,7 nS, измеренное время задержки равно 15,2 nS, разница обусловлена погрешностью метода.
Давайте к другому концу кабеля подключим подстроечный резистор и посмотрим как будет изменяться осциллограмма в зависимости от сопротивления.
При совпадении сопротивления резистора с волновым сопротивлением кабеля, вся энергия сигнала будет беспрепятственно переходить из линии в резистор и "ступенька", которая возникала за счёт отражённого сигнала, должна исчезнуть.
Сопротивление резистора 0 Ohm.

Сопротивление резистора 50 Ohm.

Сопротивление резистора 75 Ohm.

Сопротивление резистора 100 Ohm.

Из этих осциллограмм нельзя сделать однозначный вывод, какое волновое сопротивление этого кабеля.
Если увеличить длину кабеля, увеличится время задержки и изменение сопротивления на конце линии будет более наглядно. Длинного куска кабеля под рукой нет, но есть кабель, проложенный по плинтусу из одного помещения в другое. Подключил этот кабель к осциллографу с генератором.

Длина "ступеньки" увеличилась, подпаиваем с другого конца сопротивление и начинаем крутить.
Сопротивление резистора 0 Ohm.

Сопротивление резистора 50 Ohm.

Сопротивление резистора 75 Ohm.

Сопротивление резистора 100 Ohm.

Из осциллограмм видно, что волновое сопротивление кабеля равно 75 Ohm, при других значениях сопротивления "ступенька" снова появлялась.
Опираясь на полученные знания можно вычислить скорость распространения сигнала, в любой другой линии передачи данных, измерив задержку в двухметровом куске. А зная скорость можно описанным способом вычислить длину более длинного кабеля.
Теперь мы знаем как измерить длину кабеля и его волновое сопротивление с помощью осциллографа.
Похожие статьи