Как из шима получить постоянное напряжение.
Как получить из шима постоянное напряжение, знает каждый начинающий электронщик. Всё просто, надо пропустить шим через фильтр низких частот(в простейшем случае RC цепочка) и на выходе фильтра получим постоянное напряжение, не так ли?
На самом деле, как мне кажется всё гораздо интереснее, при попытке получить из шима постоянное напряжение появляются следующие вопросы:
Как подобрать номиналы элементов фильтра?
Сгладиться ли шим полностью или останутся пульсации?
И как вообще это работает, ведь конденсатор заряжается и разряжается через один и тот же резистор и по идее если коэффециент заполнения будет меньше половины, напряжение на конденсаторе вообще будет равно нулю. Например, у нас коэффециент заполнения равен 30%, тогда 30% периода конденсатор будет заряжаться, а 70% разряжаться, через тот же резистор и в итоге на нём ничего не останется, по крайне мере можно так подумать.
Давайте проверим это на практике, для этого соберём схему, изображённую ниже и подключимся щупами осциллографа в точки 1 и 2, надо отметить что период шима на порядок больше постоянной времени данной цепочки.
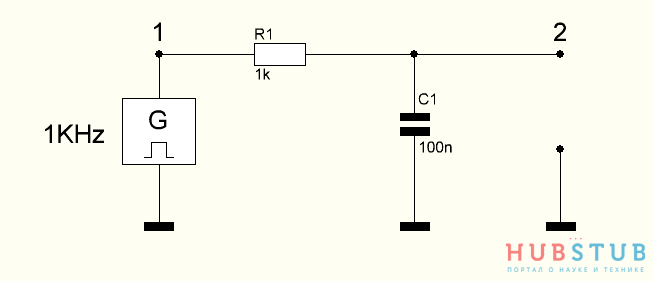
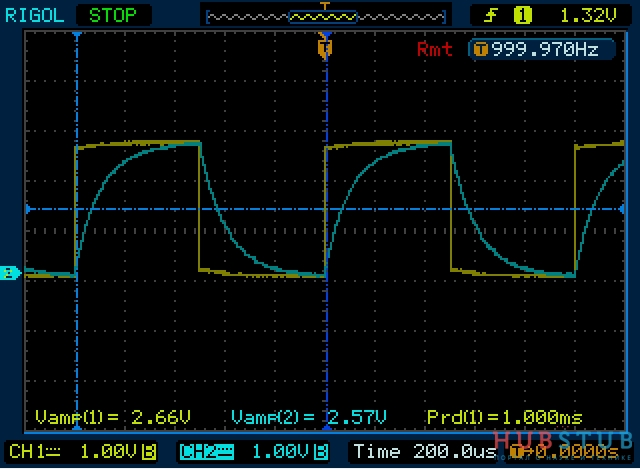
На осциллограмме видно, что действительно так и происходит, как быстро конденсатор зарядился также быстро и разрядился. Как же вообще получают постоянное напряжение из шима?
Единственная идея, которая напрашивается — это изменить номиналы RC фильтра, давайте на порядок увеличим значение резистора, тем самым увеличив постоянную RC цепи(теперь она будет равна периоду шима) или уменьшив частоту среза фильтра.
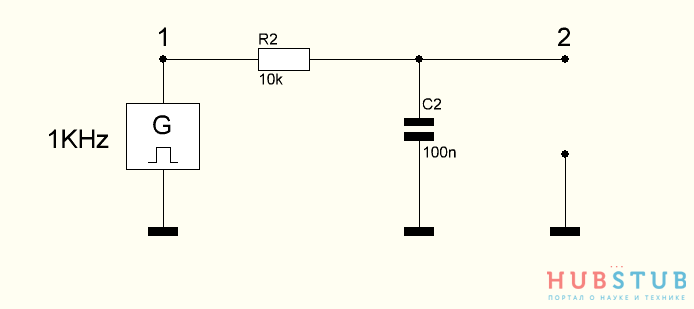
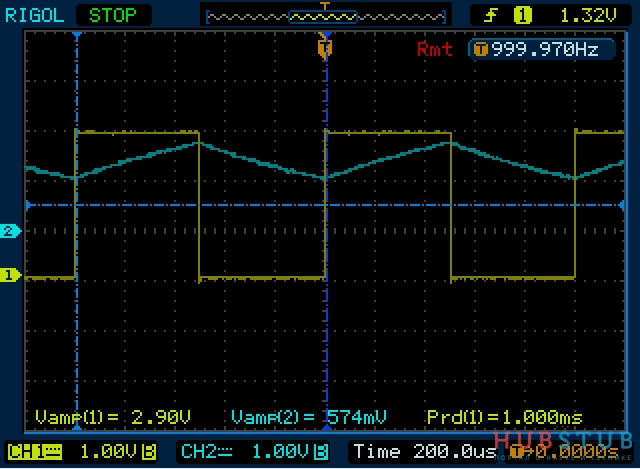
Ух ты, что-то начинает проясняться, у нас появилась постоянная составляющая. То есть в наши рассуждения закралась ошибка и заключается она в том, что конденсатор заряжается от 0 до 63% за время равное R*C(T), а разряжается он от 63% до 5% за время больше чем 2T , ниже графики, поясняющие это.
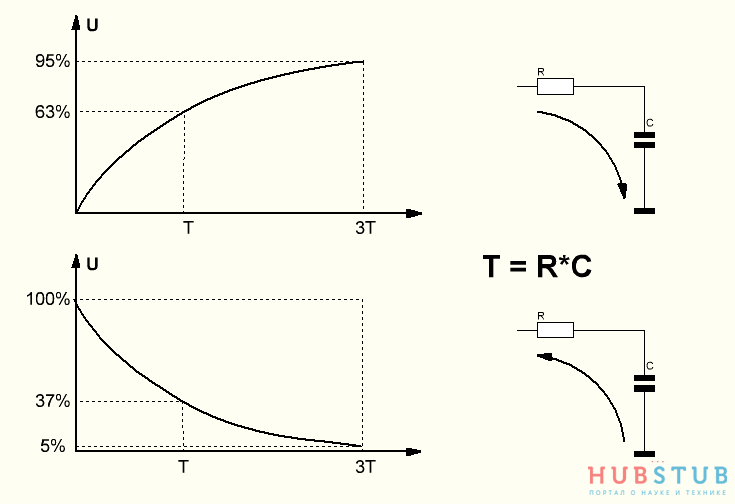
На графиках видно, что скорость зарядки и разрядки конденсатора не постоянна и зависит от заряда конденсатора, это свойство и позволяет получать из шима постоянное напряжение.
Теперь, когда мы нашли ошибку в наших размышлениях давайте, проанализируем что происходило, в первом эксперименте. Известно, что полная зарядка или разрядка конденсатора происходит за время равное 5T, а зарядка до 95% и разрядка до 5% примерно за 3T. Так как постоянная времени RC цепочки(которую мы использовали как ФНЧ) была мала, то за один период шима конденсатор успевал, почти полностью зарядиться и разрядиться.
После того как мы увеличили постоянную времени цепочки, скорость его зарядки и разрядки стала разной. Например, конденсатор успел разрядиться до 63% за время х, чтобы полностью разрядиться ему надо время превышающее 2х. Чтобы понять это можно посмотреть на графики выше.
Итак вывод, постоянная времени RC цепочки должна быть равна или больше периода шима, тогда за один период не будет происходить полный заряд-разряд конденсатора. Если же ещё на порядок увеличить постоянную времени RC цепочки, то увеличится время переходного процесса и уменьшаться пульсации. Время переходного процесса — это промежуток времени, за которое напряжение на конденсаторе изменится от 0 до некоторой постоянной величины. Данный вывод приведен для общего понимания.
Теперь примерно, понимая как вообще получают из шима постоянное напряжение, давайте перейдём к реальной задаче.
Необходимо на одном из входов ОУ формировать опорное напряжение с помощью шима и ФНЧ, логическая единица у шима составляет 3 вольта, частота шима 10KHz, допустимый уровень пульсаций 30 милливольт. Считаем, что входы ОУ ток не потребляют, в качестве ФНЧ возьмём фильтр первого порядка, реализованный на RC цепочке.
Самый простой путь — это взять RC цепочку, у которой Т на два порядка больше величины шима и посмотреть какие будут пульсаций и дальше подбирать номиналы фильтра, но это есть не что иное, как метод научного тыка, а хотелось бы всё по-честному рассчитать.
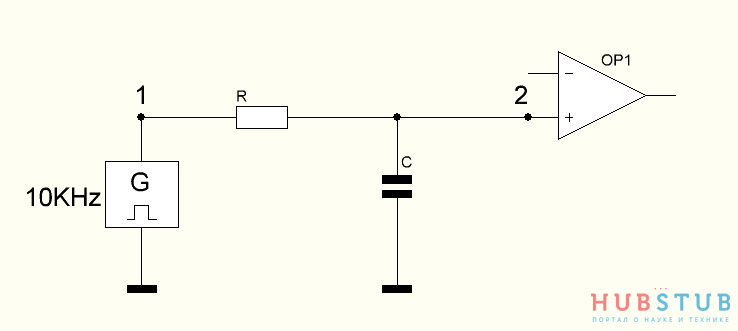
Итак для расчёта по-честному, давайте посчитаем во сколько раз надо ослабить сигнал, 3000/30 = 100 и переведём в децибелы, получается -40дб.
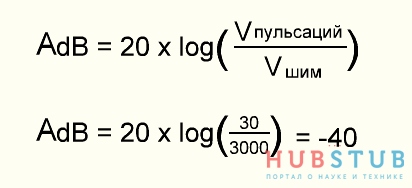
Известно, что крутизна спада у фильтра первого порядка составляет 20дб/декаду и ослабление сигнала на 40дб, соответствует увеличению частоты на две декады. (20дб/декаду - уменьшение амплитуды в 10 раз(20дб), при увеличении частоты в 10 раз(декада).
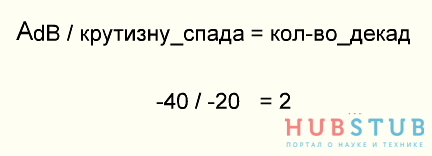
Зная, что частота среза фильтра должна быть на две декады(в 100 раз) меньше частоты шимы, можно её рассчитать 10KHz/100 = 100Hz.
Номиналы фильтра можно подобрать пользуясь известной формулой.
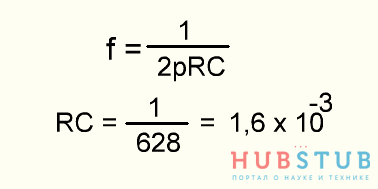
Сопротивление возьмем равным 16K, а конденсатор 100nF.
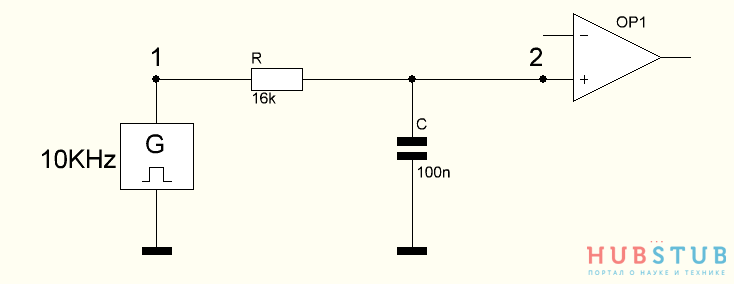
Давайте проверим, что получится на практике, соберём схему, изображённую ниже и подключимся к точкам один и два.
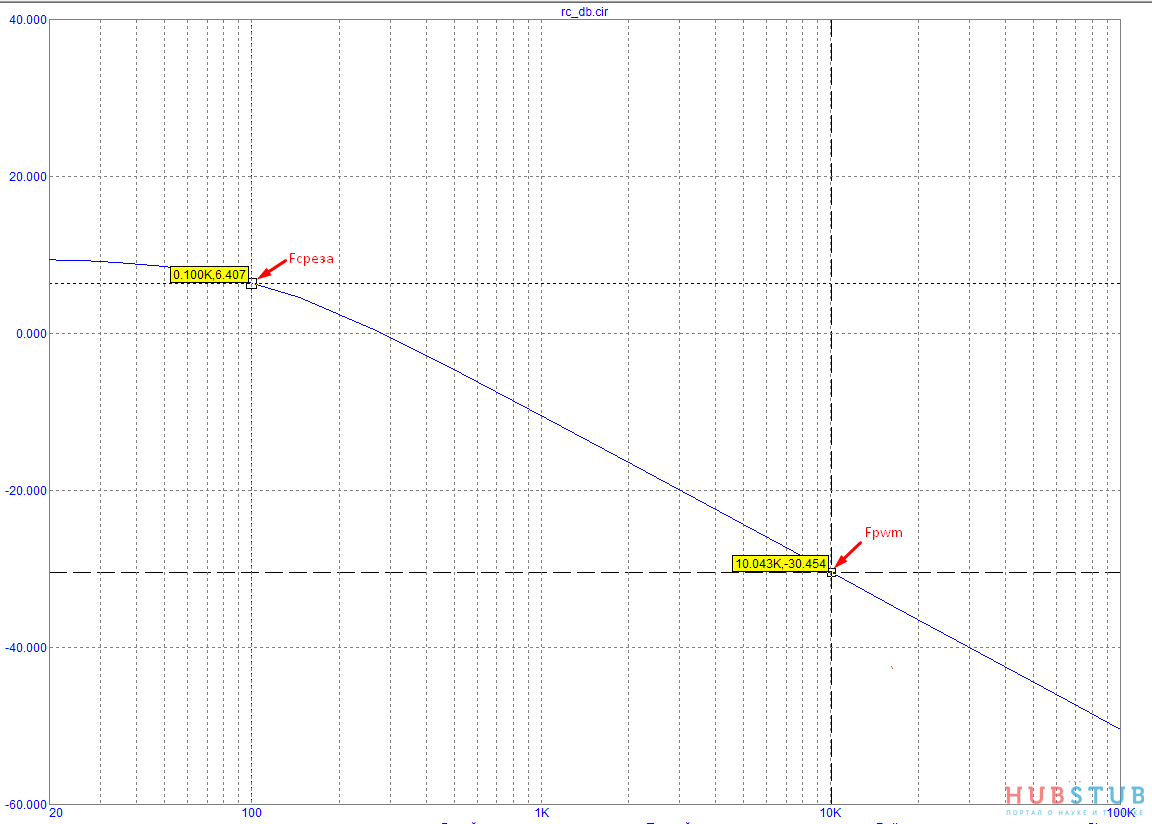
И нарисуем ЛAЧХ нашей схемы.
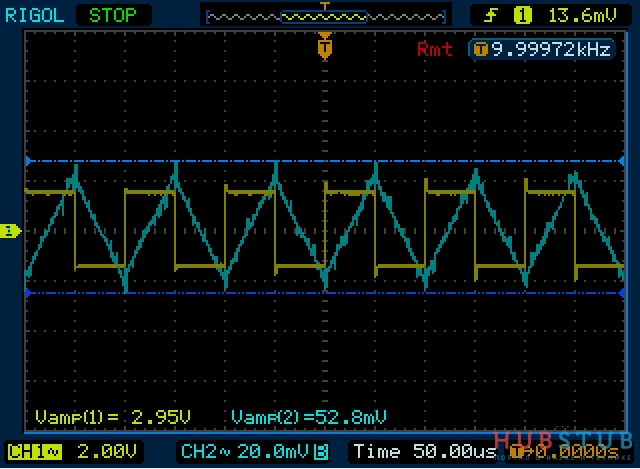
У данного генератора импульсная система питания, которая сильно шумит, это можно видеть во втором канале, но если присмотреться, то видно, что амплитуда пульсаций на осциллограмме примерно 40 милливольт, то есть немного отличается от расчётной, но это нормально так, как шим содержит высшие гармоники, которые вносят свой вклад и спад не везде равен 20дб/декаду, это видно на ЛАЧХ. Несмотря на
некоторые допущения, мне этот расчёт показался очень простым и понятным, ведь мы с помощью простых логических размышлений и школьных формул, решили такую интересную задачу. При решении данной задачи важно понять именно физический смысл, что мы по сути на АЧХ абстрактного фильтра находим точку, которая соответствует нужному подавлению сигнала, вторая координата точки - это частота, она должна быть равна частоте шима. Таким образом мы находим одну из точек АЧХ фильтра, пользуясь этой точкой находим частоту среза, а зная её мы находим номиналы фильтра, вот и всё.
На самом деле, как мне кажется всё гораздо интереснее, при попытке получить из шима постоянное напряжение появляются следующие вопросы:
Как подобрать номиналы элементов фильтра?
Сгладиться ли шим полностью или останутся пульсации?
И как вообще это работает, ведь конденсатор заряжается и разряжается через один и тот же резистор и по идее если коэффециент заполнения будет меньше половины, напряжение на конденсаторе вообще будет равно нулю. Например, у нас коэффециент заполнения равен 30%, тогда 30% периода конденсатор будет заряжаться, а 70% разряжаться, через тот же резистор и в итоге на нём ничего не останется, по крайне мере можно так подумать.
Давайте проверим это на практике, для этого соберём схему, изображённую ниже и подключимся щупами осциллографа в точки 1 и 2, надо отметить что период шима на порядок больше постоянной времени данной цепочки.


На осциллограмме видно, что действительно так и происходит, как быстро конденсатор зарядился также быстро и разрядился. Как же вообще получают постоянное напряжение из шима?
Единственная идея, которая напрашивается — это изменить номиналы RC фильтра, давайте на порядок увеличим значение резистора, тем самым увеличив постоянную RC цепи(теперь она будет равна периоду шима) или уменьшив частоту среза фильтра.


Ух ты, что-то начинает проясняться, у нас появилась постоянная составляющая. То есть в наши рассуждения закралась ошибка и заключается она в том, что конденсатор заряжается от 0 до 63% за время равное R*C(T), а разряжается он от 63% до 5% за время больше чем 2T , ниже графики, поясняющие это.

На графиках видно, что скорость зарядки и разрядки конденсатора не постоянна и зависит от заряда конденсатора, это свойство и позволяет получать из шима постоянное напряжение.
Теперь, когда мы нашли ошибку в наших размышлениях давайте, проанализируем что происходило, в первом эксперименте. Известно, что полная зарядка или разрядка конденсатора происходит за время равное 5T, а зарядка до 95% и разрядка до 5% примерно за 3T. Так как постоянная времени RC цепочки(которую мы использовали как ФНЧ) была мала, то за один период шима конденсатор успевал, почти полностью зарядиться и разрядиться.
После того как мы увеличили постоянную времени цепочки, скорость его зарядки и разрядки стала разной. Например, конденсатор успел разрядиться до 63% за время х, чтобы полностью разрядиться ему надо время превышающее 2х. Чтобы понять это можно посмотреть на графики выше.
Итак вывод, постоянная времени RC цепочки должна быть равна или больше периода шима, тогда за один период не будет происходить полный заряд-разряд конденсатора. Если же ещё на порядок увеличить постоянную времени RC цепочки, то увеличится время переходного процесса и уменьшаться пульсации. Время переходного процесса — это промежуток времени, за которое напряжение на конденсаторе изменится от 0 до некоторой постоянной величины. Данный вывод приведен для общего понимания.
Теперь примерно, понимая как вообще получают из шима постоянное напряжение, давайте перейдём к реальной задаче.
Необходимо на одном из входов ОУ формировать опорное напряжение с помощью шима и ФНЧ, логическая единица у шима составляет 3 вольта, частота шима 10KHz, допустимый уровень пульсаций 30 милливольт. Считаем, что входы ОУ ток не потребляют, в качестве ФНЧ возьмём фильтр первого порядка, реализованный на RC цепочке.
Самый простой путь — это взять RC цепочку, у которой Т на два порядка больше величины шима и посмотреть какие будут пульсаций и дальше подбирать номиналы фильтра, но это есть не что иное, как метод научного тыка, а хотелось бы всё по-честному рассчитать.

Итак для расчёта по-честному, давайте посчитаем во сколько раз надо ослабить сигнал, 3000/30 = 100 и переведём в децибелы, получается -40дб.
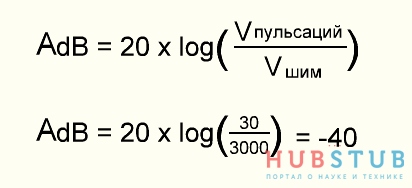
Известно, что крутизна спада у фильтра первого порядка составляет 20дб/декаду и ослабление сигнала на 40дб, соответствует увеличению частоты на две декады. (20дб/декаду - уменьшение амплитуды в 10 раз(20дб), при увеличении частоты в 10 раз(декада).
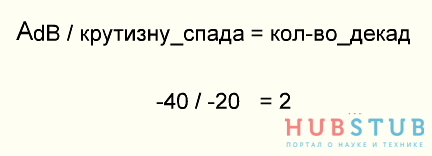
Зная, что частота среза фильтра должна быть на две декады(в 100 раз) меньше частоты шимы, можно её рассчитать 10KHz/100 = 100Hz.
Номиналы фильтра можно подобрать пользуясь известной формулой.
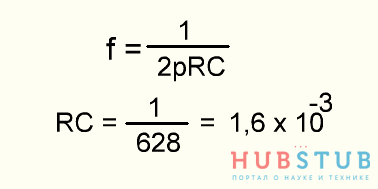
Сопротивление возьмем равным 16K, а конденсатор 100nF.
Давайте проверим, что получится на практике, соберём схему, изображённую ниже и подключимся к точкам один и два.


И нарисуем ЛAЧХ нашей схемы.

У данного генератора импульсная система питания, которая сильно шумит, это можно видеть во втором канале, но если присмотреться, то видно, что амплитуда пульсаций на осциллограмме примерно 40 милливольт, то есть немного отличается от расчётной, но это нормально так, как шим содержит высшие гармоники, которые вносят свой вклад и спад не везде равен 20дб/декаду, это видно на ЛАЧХ. Несмотря на
некоторые допущения, мне этот расчёт показался очень простым и понятным, ведь мы с помощью простых логических размышлений и школьных формул, решили такую интересную задачу. При решении данной задачи важно понять именно физический смысл, что мы по сути на АЧХ абстрактного фильтра находим точку, которая соответствует нужному подавлению сигнала, вторая координата точки - это частота, она должна быть равна частоте шима. Таким образом мы находим одну из точек АЧХ фильтра, пользуясь этой точкой находим частоту среза, а зная её мы находим номиналы фильтра, вот и всё.
Похожие статьи



