STM32 быстрое преобразование Фурье.
Давно хотелось прикрутить к осциллографу, который описывал тут, преобразование Фурье, но почему-то руки не доходили. Совсем недавно, месяц назад решил увеличить частоту сэмплирования ослика, заменив stm32F103VE с частотой сэмплирования 1М на stm32F303VC c частотой сэмплирования 5М. После замены чипа и изменения программы решил всё-таки разобраться с быстрым преобразованием Фурье(БФП или FFT).
Можно попробовать написать БФП самому, но это займет много времени, поэтому решил воспользоваться библиотекой CMSIS-DSP, но теорию всё-таки пришлось подтянуть.
У нас есть АЦП, которое с некоторой частотой отдаёт нам результаты преобразования. Мы накапливаем эти результаты в буфер перед тем, как подать их на вход БФП. Размер буфера должен быть кратен степени двойки и содержать 128(2 в 7),256(2 в 8) отсчётов и тд.
От количества точек, участвующих в БФП, зависит разрешающая способность.
Для нахождения шага между гармониками мы просто делим частоту дискретизации на количество точек, участвующих в БФП. Если при частоте дискретизации 512KHz в БФП участвует 256 точек, мы получим амплитуды гармоник с шагом 2КHz. Если же точек будет 512, то получим амплитуды гармоник с шагом 1КHz.
И ещё один пример для закрепления.
Например, при частоте дискретизации 1MHz и количестве точек 1024, спектральный отсчёт с номером 512 будет соответствовать частоте 500KHz.
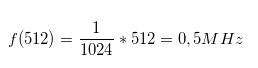
Как писалось выше, на вход БФП мы подаём вещественный сигнал, то есть данные полученные с АЦП, а на выходе получим комплексные числа, причём их будет в два раза больше. С теорией всё, предлагаю перейти непосредственно к реализации БФП на STM32.
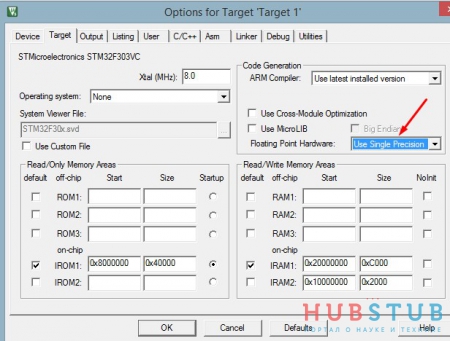
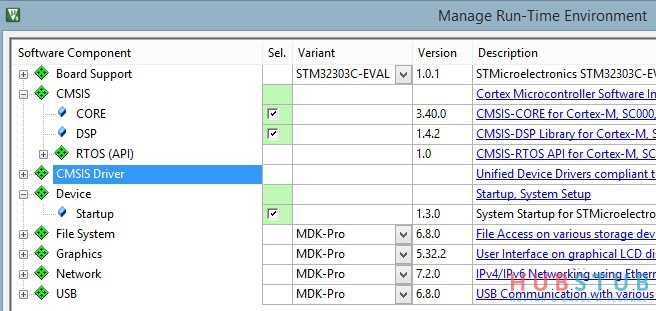
Для начала надо подключить библиотеку и включить поддержку FPU.
Теперь можно приступать к написанию программы. Код представленный ниже для STM32F303.
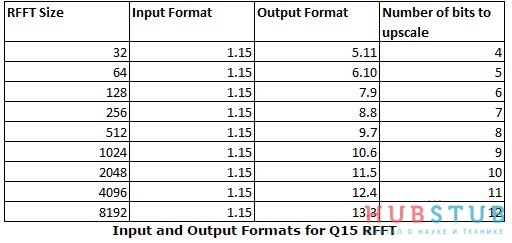
Надо отметить, что формат входных и выходных данных отличается, как показано в таблице.
Это надо учитывать при построении графика.
Вот, что получилось в итоге.
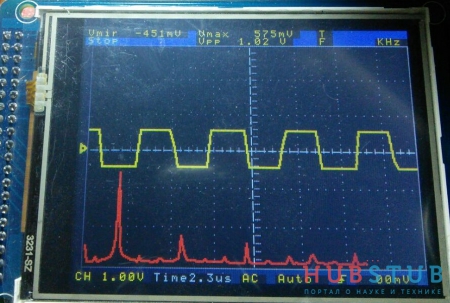
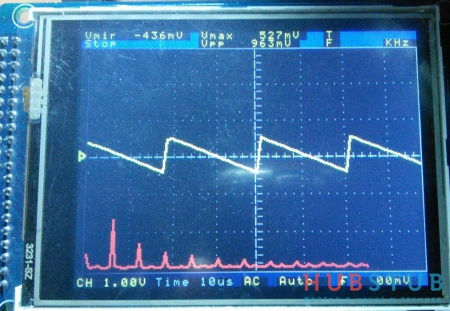
Хотелось бы напомнить, что результат БФП вещественного сигнала симметричен относительно нулевой частоты и на дисплей выведена только половина спектральных отсчётов(с 0 по 128).
Можно попробовать написать БФП самому, но это займет много времени, поэтому решил воспользоваться библиотекой CMSIS-DSP, но теорию всё-таки пришлось подтянуть.
У нас есть АЦП, которое с некоторой частотой отдаёт нам результаты преобразования. Мы накапливаем эти результаты в буфер перед тем, как подать их на вход БФП. Размер буфера должен быть кратен степени двойки и содержать 128(2 в 7),256(2 в 8) отсчётов и тд.
От количества точек, участвующих в БФП, зависит разрешающая способность.
Для нахождения шага между гармониками мы просто делим частоту дискретизации на количество точек, участвующих в БФП. Если при частоте дискретизации 512KHz в БФП участвует 256 точек, мы получим амплитуды гармоник с шагом 2КHz. Если же точек будет 512, то получим амплитуды гармоник с шагом 1КHz.
И ещё один пример для закрепления.
Например, при частоте дискретизации 1MHz и количестве точек 1024, спектральный отсчёт с номером 512 будет соответствовать частоте 500KHz.
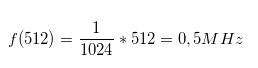
Как писалось выше, на вход БФП мы подаём вещественный сигнал, то есть данные полученные с АЦП, а на выходе получим комплексные числа, причём их будет в два раза больше. С теорией всё, предлагаю перейти непосредственно к реализации БФП на STM32.
Для начала надо подключить библиотеку и включить поддержку FPU.

Теперь можно приступать к написанию программы. Код представленный ниже для STM32F303.
#define ARM_MATH_CM4// указываем на каком ядре построен МК
#include <arm_math.h> //подключаем библиотеку
#define FFT_SIZE 256//указываем размер FFT
//Создаём два буфера, в одном будем хранить выборки АЦП, во втором результаты БФП
q15_t fft_Sbuff[FFT_SIZE] = {0};
q15_t fft_Dbuff[FFT_SIZE*2] = {0};
uint16_t k;
uint8_t status;
arm_rfft_instance_q15 S;
status = arm_rfft_init_q15(&S, FFT_SIZE, 0, 1);//функция инициализации необходима для БФП
if(status == ARM_MATH_SUCCESS)
{
arm_rfft_q15(&S,fft_Sbuff, fft_Dbuff);//выполнение БФП
arm_cmplx_mag_q15(fft_Dbuff, fft_Sbuff, FFT_SIZE);//вычисляем амплитуды гармоник
}
Надо отметить, что формат входных и выходных данных отличается, как показано в таблице.

Это надо учитывать при построении графика.
Вот, что получилось в итоге.


Хотелось бы напомнить, что результат БФП вещественного сигнала симметричен относительно нулевой частоты и на дисплей выведена только половина спектральных отсчётов(с 0 по 128).
Похожие статьи