Восстановление сигнала методом Digital Lock-in Amplifier.
В школе, на уроках математики, нас учили по виду кривой описывать ее уравнением. Для человека такая задача считается простой, но если попробовать переложить эту задачу на микроконтроллер, мы увидим, что даже синусоидальный сигнал распознать не так просто.
Давайте представим, что мы подали синусоидальный сигнал на вход АЦП и собрали несколько десятков выборок. Если эти выборки нарисовать на листе бумаги, мы с легкостью определим амплитуду, фазу и частоту, а используя их, напишем уравнение кривой, типа A*sin(wt+q). Используя же МК, мы с легкостью рассчитаем амплитуду, как разность между большим и меньшим значением и частоту, которую можно вычислить разными способами. А как рассчитать фазу?
Оказывается простого решения этой задачи не существует и для этого потребуется чуть более сложная математика. Далее, мы рассмотрим одни из вариантов решения этой задачи, который известен как Digital Lock-in Amplifier.
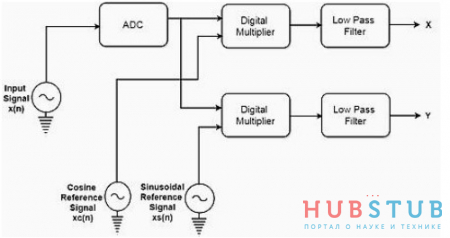
Суть его заключается в том, что данные, полученные с АЦП, мы по сути пропускаем через два миксера, в которых они(данные) перемножаются с известными опорными сигналами, а далее эта смесь пропускается через ФНЧ. На данном этапе надо понимать, что опорные сигналы хранятся в памяти МК в виде массивов, для заданной ПЧ.
Теперь, когда общая концепция ясна, предлагаю рассмотреть математику процесса. Для этого нам понадобится еще одна картинка.
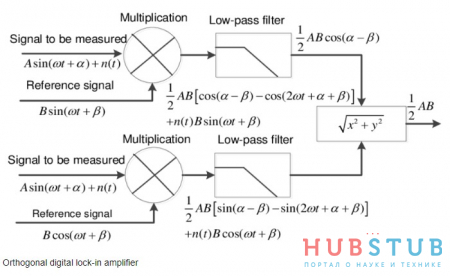
Из картинки понятно, что сигнал, поступающий на АЦП представляем в виде A*sin(wt+q), а опорные сигналы как B*cos(wt+p) и B*sin(wt+p). Хотелось бы, отметить, что сигнал с АЦП также можно представить в виде A*cos(wt+q), мы так и поступим.
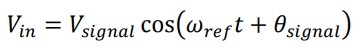
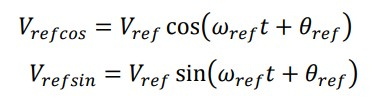
На первом этапе, как уже упоминалось раньше, смешиваем сигнал, пришедший с АЦП, с опорными сигналами. Для этого вспомним необходимые тригонометрические формулы.
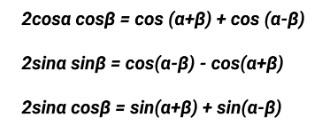
И воспользуемся ими.
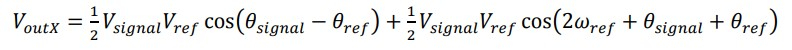
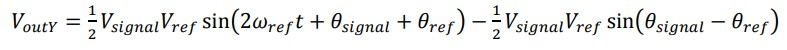
На следующем шаге мы должны пропустить оба сигнала через ФНЧ, в результате чего будут подавлены высшие гармоники и формулы примут вид.
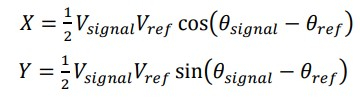
Полученные компоненты можно использовать для вычисления амплитуды
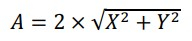
и фазы.
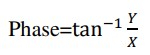
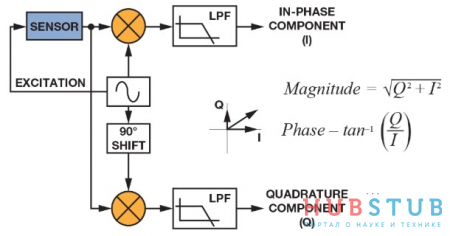
Частота в данном случае известна и ее вычислять не надо. Также оставлю еще одну картинку, поясняющую откуда взялись формулы.
Может создаться впечатление, что для вычислений достаточно одного измерения, но это не так. Мы рассмотрели лишь общую схему алгоритма, упуская тонкости реализации.
Давайте представим, что мы подали синусоидальный сигнал на вход АЦП и собрали несколько десятков выборок. Если эти выборки нарисовать на листе бумаги, мы с легкостью определим амплитуду, фазу и частоту, а используя их, напишем уравнение кривой, типа A*sin(wt+q). Используя же МК, мы с легкостью рассчитаем амплитуду, как разность между большим и меньшим значением и частоту, которую можно вычислить разными способами. А как рассчитать фазу?
Оказывается простого решения этой задачи не существует и для этого потребуется чуть более сложная математика. Далее, мы рассмотрим одни из вариантов решения этой задачи, который известен как Digital Lock-in Amplifier.
Суть его заключается в том, что данные, полученные с АЦП, мы по сути пропускаем через два миксера, в которых они(данные) перемножаются с известными опорными сигналами, а далее эта смесь пропускается через ФНЧ. На данном этапе надо понимать, что опорные сигналы хранятся в памяти МК в виде массивов, для заданной ПЧ.
Теперь, когда общая концепция ясна, предлагаю рассмотреть математику процесса. Для этого нам понадобится еще одна картинка.
Из картинки понятно, что сигнал, поступающий на АЦП представляем в виде A*sin(wt+q), а опорные сигналы как B*cos(wt+p) и B*sin(wt+p). Хотелось бы, отметить, что сигнал с АЦП также можно представить в виде A*cos(wt+q), мы так и поступим.
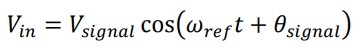
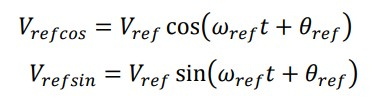
На первом этапе, как уже упоминалось раньше, смешиваем сигнал, пришедший с АЦП, с опорными сигналами. Для этого вспомним необходимые тригонометрические формулы.
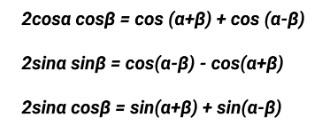
И воспользуемся ими.
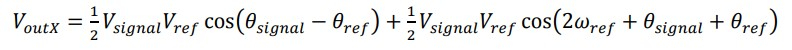
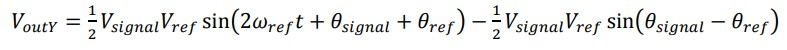
На следующем шаге мы должны пропустить оба сигнала через ФНЧ, в результате чего будут подавлены высшие гармоники и формулы примут вид.
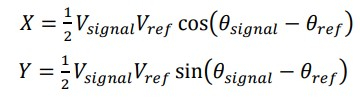
Полученные компоненты можно использовать для вычисления амплитуды
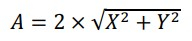
и фазы.
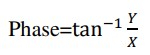
Частота в данном случае известна и ее вычислять не надо. Также оставлю еще одну картинку, поясняющую откуда взялись формулы.
Может создаться впечатление, что для вычислений достаточно одного измерения, но это не так. Мы рассмотрели лишь общую схему алгоритма, упуская тонкости реализации.
Похожие статьи